The Exponentiation And Its Properties.

Exponentiation is a mathematical operation, written an, involving two numbers, the base a and the exponent n. When n is a positive integer, exponentiation corresponds to repeated multiplication:



The exponent is usually shown as a superscript to the right of the base. The exponentiation an can be read as: a raised to the n-th power, a raised to the power [of] n or possibly a raised to the exponent [of] n, or more briefly: a to the n-th power or a to the power [of] n, or even more briefly: a to the n. Some exponents have their own pronunciation: for example, a2 is usually read as a squared and a3 as a cubed.


Exponentiation Properties

Exponentiation properties allow to resolve powers by different methods. These are:

Power of exponent 0

Every power of exponent 0 and base different of 0 is 1.

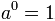if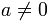

Power of exponent 1

Every power of exponent 1 is equal to the base.

Example:



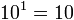
Product of powers with the same base

For the product of two or more powers with equal base you put the same base and add up the exponents.



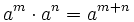
Example:



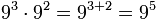
Division of powers with the same base

In the division of two powers with equal base you put the same base and subtract the exponents.



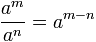
Power of a product

The power of a product with base (a•b) and exponent "n" is equal to the power "a" to the "n", "b" a la "n" times. You multiply each base the times of the exponent.



Power of a division

In the power of a division with base "a/b" and exponent "n" you raise each of the components of the base to the "n".



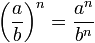
Power of a power

To resolve the power of a power you put the same base and multiply the exponents.



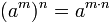
Distributive property

Exponentiation is distributive in relation to the multiplication and division, but it is not in relation neither to the sum nor the subtraction.

Distributive in relation to the multiplication and division:



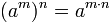
It is not distributive in relation to the sum and subtraction:




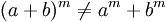
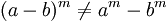
Commutative property

The commutative property does not exist for the exponentiation, excluding these cases in where the base and the exponent have the same value or they are equivalents.

In general:



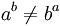
Associative property

The associative property does not exist for the exponentiation.



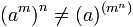
Powers of ten

Every power of ten with a natural number as exponent is equal to the unit followed of the quantity of zeros that the exponent indicates.





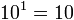
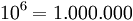
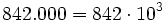
Powers of fractional exponent

It is a power that has its exponent in form of a fraction, and here you see that:



Power of a negative exponent
When you see a power that has negative exponent you change the place and by this way its exponent automatically will be positive.
a − b = 1 / ab

I hope you have learned!



EXERCISES

With the following exercises you can practice the contents learned. Click the links and prove you have learned!

http://maralboran.org/web_ma/descartes/1y2_eso/potencia/prueba_3.html
http://maralboran.org/web_ma/descartes/1y2_eso/potencia/producto_1.html
http://maralboran.org/web_ma/descartes/1y2_eso/potencia/cociente_1.html
http://maralboran.org/web_ma/descartes/1y2_eso/potencia/potpot_1.html
http://maralboran.org/web_ma/descartes/1y2_eso/potencia/potprod_1.html
http://maralboran.org/web_ma/descartes/1y2_eso/potencia/prueba_2.html

Now you know all that you need to know about exponentiation!

Good Luck!